The physics of maXair

Dave Althoff, Jr.
March 18, 2005

maXair is at first glance a very simple ride. It consists of an 82-foot-long pendulum suspended from an 85-foot frame. At the base of the pendulum is a gondola ring with 25 pairs of seats. The pendulum is driven by a grouping of six electric motors, but to the degree that it is possible to do so, it is pushed at its normal harmonic frequency. So the ride action describes that of a simple pendulum. The gondola ring rotates at 8 RPM, so that every passenger gets an ever-changing view throughout the ride.

First things first

In studying this ride, there is something we need to keep in mind. There is one force which has a significant impact on the ride, namely gravity. At every point on the ride, gravity is doing its thing.

Gravity is a fundamental force of nature. It is an attractive force which exists between all objects, and it can be described mathematically through Newton’s Law of Universal Gravitation, which states that the force exerted by gravity is equal to the Universal Gravitational Constant (G) multiplied by the product of the masses of the two objects and divided by the square of the distance between them.

In other words

It just so happens that most places on the Earth, the largest object that can exert a gravitational force on anything you might find happens to be the Earth itself. Furthermore, the difference in the masses of the Earth and almost any object on the Earth is extremely large, and the distance from the surface to the Earth’s center of mass is (to a reasonable number of significant figures) fairly constant. This leads to a very useful simplification for the special case of comparatively small masses (even to hundreds of tons; this is 'small’ compared to the mass of the Earth!) near the surface of the Earth-- F = mg where g = 32 ft/sec/sec, in accordance with Newton’s second law (Force = mass*acceleration) F[pounds] = m[slugs]*g[feet/second/second]

For our purposes, we can simplify things even further, because for theoretical purposes at least, the masses all remain constant in the systems we are studying. Ignoring the occasional blown lunch or...well, we hope we don’t have any of those either...the mass of the system should remain constant while we’re studying it, that is, during the course of the ride. So to understand the forces, all we really need to consider are the accelerations. If we multiply the acceleration by the mass, we will get the actual force. Or, if we compare the acceleration to the acceleration component of the force supplied by gravity near the surface of the Earth, we get a G-force. Got that? A G, then, is a unitless (often used itself as a unit) multiplier used to relate a force to what gravity would do in a familiar setting. That’s useful because it recognizes that mass is an important component of force, but allows us to safely ignore mass in writing the equations so long as the mass remains constant.

Neat, huh?

Gravity has a couple of other neat features that are going to be very important to us. The most important is that it not only provides a constant magnitude of acceleration, it is also always applied in the same direction: directly towards the center of the Earth, or if you prefer, straight down. Just looking at a pendulum you can see that this is important, can’t you? This is, after all, what drives the motion of a pendulum. When the pendulum is going up, gravity tries to bring it back down. When gravity finally wins out, it accelerates the pendulum down to its bottom center point, then retards its progress back up the other side. But I am getting ahead of myself.

Rotation

The seats on maXair are mounted on a gondola ring which rotates at 8 RPM. For reference, that is about the same speed as the main center rotation on the Monster, or about double the rotating speed of the Midway Carousel. The odd thing about that is that on maXair, the seats face outward. When I heard this, my first concern was that it would be rather unpleasant to ride with all that force applied outward. I ran some calculations. The outward force felt by a rider at 8 RPM on a 44-foot diameter ring is going to be about 15 ft/sec/sec, or about half a G.

Gravity to the rescue!

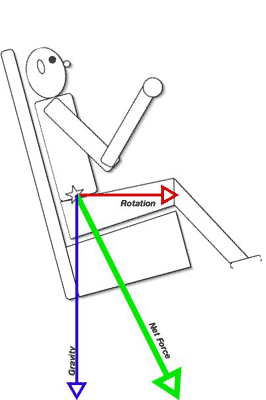
Figure 1

Huss considered this in their design, and came up with a clever solution. As you can see in the accompanying drawing, the seat is tipped back at about a fifteen-degree angle. When you add the outward half-G force to the downward 1-G force, the result is a force equal to about 1.1G applied downward and outward at about 25 degrees. Graphically (Figure 1) you can see that it lines up very nicely right through the bottom of the seat.

Incidentally, remember this 15-degree tilt because it is going to be a factor later!

Swinging

According to Huss, maXair is accelerated by its six electric motors and reaches its full height in about 40 seconds. For our purposes, it is after it reaches full height and speed that things really get interesting. At that point, so the manufacturer claims, the ride emulates a mathematical pendulum, which means we can predict what it is doing. It’s reasonable that the manufacturer would program the ride to follow its natural pattern, as that allows gravity to do most of the heavy lifting (so to speak), and a minimal amount of torque from the motors will maintain full swing against the resistive forces trying to bring it to a stop.

Why is this interesting?

Have a look at what maXair is doing. As it rotates through its full 240 degree arc, its velocity changes continuously. As a result, the angular velocity is not constant, its tangential speed is not constant, and the outward ("down" relative to the seat) changes continuously.

maXair is designed to operate as a mathematical pendulum. A simple pendulum with a length of 82 feet will have a period of about ten seconds. In reality, it isn’t all that simple because the magnitude of oscillation is 240 degrees, the pendulum shaft has significant mass, and the whole thing is driven by a set of six electric motors. Rather than calculating the ride velocities, I’m going to take the manufacturer’s word for the maximum: they claim that as the ride comes through its center point, its top speed is 65 MPH including the gondola rotation, and the maximum force is 4.5G. We can do a quick sanity check on that...65 MPH is about 95.33 feet/second, and the rotation amounts to 18.43 feet per second. Subtract the rotation from the swing, and you get the swing rate of the center of the gondola, which would be about 76.9 feet/second, which amounts to 52.43 MPH.

The interesting thing about this is that because the gondola is rotating, your velocity as you pass through the fastest point of the swing...that is, when the pendulum reaches bottom-dead-center...will be dependent on your position around the ring. If you are facing the swing axis, your speed will be 76.9 feet per second. If you are on the side moving in the same direction as the swing, you’ll be moving at 95.33 feet per second, and if you’re on the opposite side, your speed could be as low as 58.47 feet per second.

Okay, so it’s time for more math. The linear acceleration felt by a rider is going to be equal to v^2/r. The radius here is 82 feet. So for each of the 'extreme’ seating positions, the force is going to be... Slowest seat: (58.47)^2/82 = 41.69 ft/sec^2 = +1.30 G?End seat: (76.90)^2/82 = 72.12 ft/sec^2 = +2.25 G?Fastest seat: (95.33)^2/82 = 110.83 ft/sec^2 = +3.46 G

But wait! There’s more!

Remember, gravity is still there, meaning those values should be +2.30 G, +3.25 G, and +4.46 G respectively. I can live with those numbers; the manufacturer claims a maximum acceleration of +4.5G at the bottom of the swing.

Don’t forget!

Figure 2

Remember also that the seat is inclined backward at 15 degrees, and we still have that outward force of about half a G. But if you have a look at the second diagram, which shows the minimum forces acting on a rider at the bottom center of the swing, you can see that as the vertical force gets larger, the net force (green line) aligns more precisely with the rider’s spine. (Figure 2)

Figure 3

At the other end of the swing, the situation is a bit different. The ride reverses direction, which means that at the peak of the swing, there is no tangential acceleration at all. This means the swinging motion does not pull the rider "down" into his seat at all. The gondola is still rotating, so there is still that half-G outward acceleration. But gravity is now pulling in what certainly appears to be the wrong direction. The rider feels the outward force pulling "down" and outward at half a G at a fifteen degree angle. Gravity is pulling "down" 1G at a 135 degree angle...which is to say, it’s actually pulling "up" 1G at a 45-degree angle. Resolving all of that, I get a net force pulling "back" at about 0.22G and "up" at 0.58G. That means the green line in that diagram is, so far as the rider is concerned, pulling him up and back with a force of 0.63G at a 69 degree angle. Remember, this is from the rider’s point of view, where "level" is actually inclined fifteen degrees back from the horizontal axis of the gondola ring. (Figure 3)

All of that happens over the course of about ten seconds. The rider goes from a true negative 0.62 G experience at the top of the swing to a crushing 4.4 G at the bottom, then back down to -0.62 again at the top on the other side. So the vertical force changes continuously. Add to that, the rotation also causes some interesting angles to appear that I’ve simply ignored by only considering the four 'corner’ seat positions. The ride motions are entirely periodic, everything is very simple, but for any given rider, the rotation means the exact location around the ring will be different at any given point on each swing. That means the forces you feel riding maXair will vary continuously, in a non-repeating pattern through the entire ride.